[삼성 SDS Brightics] 회귀① - 단순선형회귀모형(Linear Regression)-부모의 키는 자식에게 유전될까?

안녕하세요! yeenn입니다.
무사히 brightics 홍보영상미션도 마무리되어서 이제는 팀 분석 미션을 준비중에 있는데요..!
(사실 아직 제작한 영상이 유튜브 업로드 전이라..조금 떨리네요ㅎ과연 내 얼굴을 내가 똑바로 볼 수 있을지..)
팀 분석미션을 위한 분석 및 영상 기획안도 차츰차츰 완성되어가는 중이니, 추후 포스팅도 많은 기대 부탁드립니다!
이번에 포스팅할 주제는 '단순선형회귀'인데요,
앞으로 당분간 미션포스팅과 더불어 브라이틱스로 회귀분석을 하는 과정을 포스팅해볼 계획입니다!
[이론학습]
선형회귀란?
선형회귀(linear regression)란,
독립변수과 종속변수의 관계를 선형인 함수로 가정할 수 있는 경우의 회귀분석을 뜻합니다.
상관관계가 두 변수 사이의 전체적인 관련 강도를 측정하는 것이라면,
회귀는 관계 자체를 정량화하는 방법이라는 점에서 차이가 있다고 볼 수 있습니다!

회귀모델은 위와 같이 구분을 할 수 있는데요,
독립변수가 1개이면 단순회귀(Simple Regression),
독립변수가 2개이상 이면 다중회귀(Multiple Regression)로 분류 할 수 있으며
이에 파생되어
회귀계수(기울기, x의상수값)가 선형이면 선형회귀,
비선형이면 비선형 회귀모델로 구분을 할 수 있습니다.
그 중 독립변수가 1개인 경우의 단순선형회귀(simple linear regression)는

위와 같은 회귀함수로 종속변수가 표현될 것이라고 가정되는 회귀모형을 의미합니다.
우리에게 익숙한 직선함수를 생각하시면 될 것 같아요.
단순선형회귀분석의 가정
1. 하나의 종속 변수와 하나의 독립변수를 분석
2. 독립변수 X의 각 값에 대한 Y의 확률분포가 존재함
3. Y의 확률분포의 평균은 X값이 변함에 따라 일정한 추세를 따라 움직인다.
4. 종속변수와 독립변수 간에는 선형 함수 관계가 존재함
단순선형회귀분석은 위와 같은 4가지의 가정을 만족합니다.
선형회귀의 함수식은 자료가 생성된 프로세스가 직선 식을 중심으로 하여 임의로 생성되었을 것이라는 가정을 하고 있는데요, 그렇기 때문에 실제 자료에 대해 산점도를 그렸을 때, 직선의 형태인 것이 확인되어야 선형회귀모형을 올바르게 적용할 수 있습니다!

[실습]
자식의 키는 부모로부터 유전될까?
당연히 후천적인 요인도, 외부적인 요인도 존재하겠지만,
보통의 상식으로는 "부모의 키가 크면 자식의 키도 크다" 라고 생각되기 마련이잖아요!
(저희집도 그러한편..)
그래서 든 궁금증!
Q. 아버지의 키가 크면 아들의 키도 클까?
를 알아보기 위해
Brightics를 사용하여 회귀분석을 진행해보겠습니다!
dataset
| 변수명 | 설명 | data type |
| seq | 순번 | Double |
| father_height | 아버지의 키 | Double |
| son_height | 아들의 키 | Double |
※ 해당 포스팅은 Brightics Github에 수록된 dataset을 활용하여 작성되었습니다.
0. Data Flow Model

이번 실습의 work flow model은 위와 같습니다!
1. Data Load



아버지와 아들의 키 정보가 포함된 dataset father_son_height.csv를 load해줍니다.
설정은 default값 그대로 해주시면 됩니다!
2. 요약통계량 확인
먼저, 아버지의 키와 아들의 키 변수의 기초 요약통계량을 확인해보겠습니다.
Statistic Summary함수를 불러와,
Input Columns: father_height, son_height
을 지정해주시고,
Target statistic에 아버지와 아들의 키간 최대, 최소, 평균값을 확인하기 위해
Max, Min, Average를 선택해줍니다.

아들의 평균키가 약 171cm로, 아버지의 평균키 168cm보다 더 큰 것을 확인할 수 있었습니다!
3. 데이터 분할
그 다음, 데이터를 train data와 test data로 분리하기 위해 Split Data함수를 사용해보겠습니다.
7:3의 비율로 데이터 셋을 나누고,
seed값 123을입력해줍니다.

차례대로 위 table은 train set, 아래 table은 test set인데요,
비율대로 잘 분리가 되었는지 확인하기 위해 table을 나누어 살펴보았습니다!

Table을 Duplicate해주신 후, Chart Settings>Select Data Source에 들어가서,
각 table에 Split Data(train_table) / Split Data(test_table) 를 지정해주시면, 위와 같은 table을 확인할 수 있습니다!
4. 훈련(Linear Regression Train)
그 다음, 학습 데이터로 회귀모형을 적합하기 위해 Linear Regression Train을 활용해보겠습니다.
Feature Columns에는 설명변수 X인 father_height를,
Label Column에는 반응변수 Y인 son_height를 지정해주세요.
Fit Intercept와 VIF는 디폴트 값 그대로 설정해주시면 됩니다!
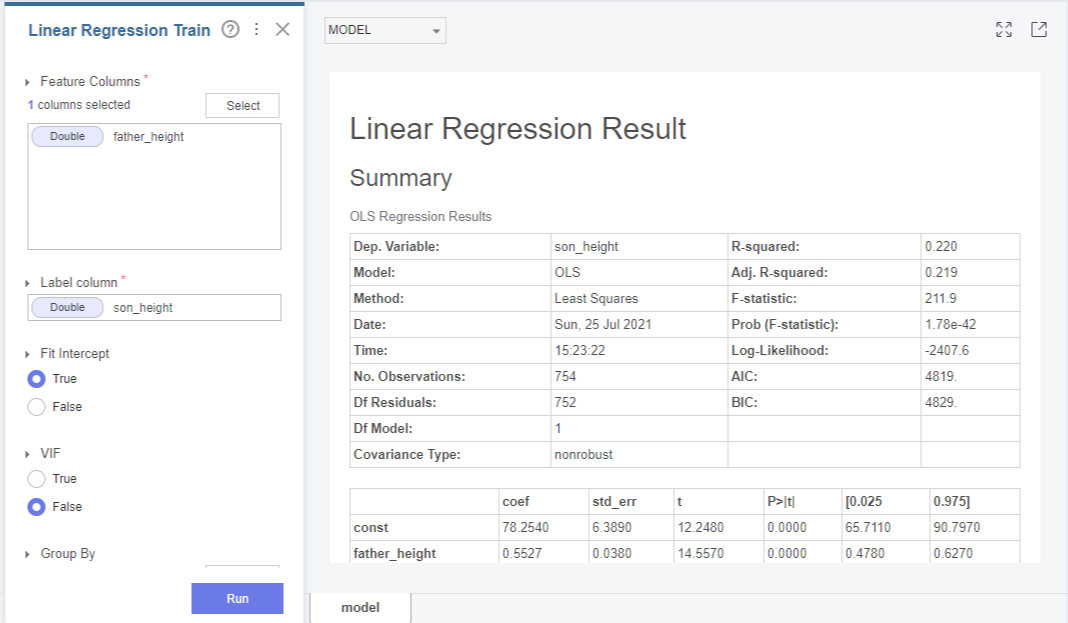
그럼 적합된 모형에 대한 요약정보가 아래와 같이 출력이 되는데요, 출력결과를 조금 더 자세히 살펴보겠습니다!

먼저 이 회귀모형이 유의한지를 확인하기 위해 p-value를 살펴보겠습니다.

F 통계량에 대한 p-value(Prob(F-statistic)가 1.78e-42로 0.05보다 작기 때문에 5% 유의수준에서 회귀모형이 유의함을 알 수 있었습니다.
다음은 R-squared 결정계수를 통해 모형의 설명력을 살펴보겠습니다.

결정계수 R-squared와 수정된 결정계수 Adj.R-squared는 모형의 설명력을 나타내는데요, 1에 가까울 수록 좋은 모형임을 나타내나 현재 모형의 설명력은 0.22로 높지 않은 것을 확인할 수 있었습니다.
그렇다면,
아들의 키 son_height를 설명하기 위한 변수가 아버지의 키 father_height외에 더 있다는 뜻이겠죠?
결정계수가 작다는 것은 곧 = 두 연속형 변수의 선형관계가 약하다
는 뜻인데요,
즉, 위 출력결과를 정리해보자면
한 직선에 모여있는 정도가 약하다는 의미이나, 모형이 유의하기 때문에 선형성은 존재한다
로 해석할 수 있겠습니다!
그 아래로는 개별 회귀계수에 대한 유의성검정을 위한 회귀계수 추정치(coef)와 t통계량, 이에 대한 P-value, 회귀계수에 대한 신뢰구간이 출력되는데요,
father_height에 회귀계수에 대한 p-value가 0.05보다 작기 때문에 5%유의수준에서
회귀계수가 유의하다고 판단할 수 있었습니다.
이를 바탕으로
"son_height = 78.25 + father_height x 0.55"
와 같은 회귀식을 도출해보았습니다!

더빈-왓슨(Durbin-Watson) 값은 0-4사이 값으로, 2에 가까울수록 자기상관이 없이 '독립'이라는 의미인데요!
이 결과표에서는 2와 가까운 값인 1.99이 나왔기 때문에 son_height의 각 관측치가 자기상관이 없이 독립성을 잘 만족한다고 볼 수 있겠습니다!
※ 위 dataset은 시계열 data가 아니기 때문에 더빗-왓슨 값을 확인할 필요는 없지만, 만약 어떤 데이터가 시계열적 성질을 가진다면, 이 값을 확인하여 자기상관이 있는지 확인하여야 합니다..!
이어서 출력된 그림을 살펴보겠습니다!

첫 번째 그림은 실제 X와 Y의 추정치에 대한 산점도인데요,
실제 Y값이 커지면 Y의 추정치도 함꼐 커지는 것으로 보아 추정치와 실제값이 선형성이 있음을 판단할 수 있었습니다!

두 번째 그림은 Y의 추정치와 잔차에 대한 산점도인데요,
모형이 랜덤하게 만들어졌기 때문에 등분산성 가정이 만족되었음을 판단할 수 있었습니다.

위 그래프는 잔차에 대한 Q-Q플롯인데요,
각 점이 대각선과 거의 일치하고 있기 떄문에 정규성이 만족되었다고 할 수 있겠습니다!

위 히스토그램 또한 정규성 가정 검토에 사용되는 차트인데요,
히스토그램의 모양이 종모양에 가깝기 때문에 마찬가지로 정규성이 만족되었다고 할 수 있습니다!
5. 예측(Linear Regression Prediction)
다음은, 회귀모형에 대한 예측치를 생성하기 위해 Linear Regression Preidct를 활용해보겠습니다.

Input table: Split Data-test_table
model: Linear Regression Train-model
이 지정될 수 있게 함수를 연결해주고 Run을 눌러주시면,
예측변수 prediction이 새로 생긴 것을 확인할 수 있습니다!
6. 모형 평가
그 다음, 실제 아들의 키와 추정된 아들의 키를 비교하기 위해,
Label Column: son_height,
Prediction Column: prediction
을 지정하고 Run을 눌러줍니다.

출력결과를 살펴보면,
모형을 비교할 수 있는 결정계수(r2_score), 평균제곱오차(mean_squared_error. MSE), 평균제곱오차제곱근(root_mean_squared_error, RMSE), 평균절대오차(mean_absolute_error, MAE), 중앙값 절대오차(median_absolute_error), 설명되는 분산점수(explained_variance_score)값이 출력됩니다!
7. 아들의 키 추정
Brightics에는 파일을 읽어오는 것이 아닌 직접 데이터를 만들어서 분석에 활용할 경우 사용하는 함수 Create Table이 있는데요, 이 함수를 활용하여 새로운 X값에 대한 Y값을 예측해보겠습니다.


Create Table함수를 불러오면, 좌측과 같은 설정창이 보이는데요, 여기서 Edit 밑의 'Open Editor'을 누르면, 우측과 같은 화면이 나옵니다.

좌상단의 table을 확대해보면, 위와 같은 그림이 나오는데요,
빨간 네모 영역에는 변수명을 입력하고 초록 네모 영역에는 값을 입력하시면 됩니다.


그 다음, 새로운 table에 좌측과 같이 새로운 아버지의 키 father_height를 입력하고, father_height의 변수명과 data type을 동일하게 입력해
줍니다!
이제 Create Table을 통해 새로 생성된 아버지의 키(father_height)에 대해 아들의 키(son_height)를 추정하기 위해, Linear Regression Predict를 사용해보겠습니다.

Creat Table 함수와 Linear Regression Train을 연결한 후, Linear Regression Predict를 불러와 다시 연결해 줍니다.
다음, Y의 새 예측치를 어떻게 저장할지 Prediction Column Name에 입력하면 되는데요,
저는 아버지 키 예측치와 구분하기 위해 son_prediction 을 입력해주었습니다.
(default 값 'prediction' 그대로 두셔도 무방합니다!)
실행결과를 살펴보니, son_prediction column에 아들의 키 추정치가 출력되는 모습을 확인할 수 있었습니다!

아버지의 키가 161.5cm인 경우, 아들의 키는 평균적으로 167.5cm,
아버지의 키가 166.3cm인 경우, 아들의 키는 평균적으로 170.1cm,
아버지의 키가 182.7인 경우, 아들의 키는 평균적으로 179.2cm인 것을 확인할 수 있었습니다!
대체적으로 170대 초반cm을 기준으로 이보다 작으면, 아버지보다 아들이 키가 크고, 이보다 크면 아버지보다 아들이 작은 양상을 보이고 있네요..! 신기신기
이상으로 단순선형회귀모형에 대한 포스팅을 마치도록 하겠습니다!
-본 게시물은 Brightics 서포터즈 활동의 일환으로 작성된 포스팅 입니다.